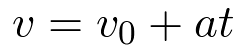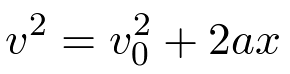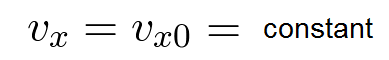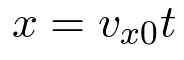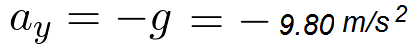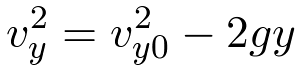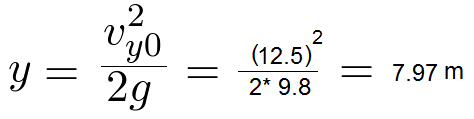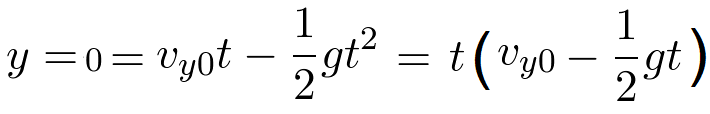Projectiles
Projectiles are objects that move with a constant horizontal velocity and are subject to the earth's gravitational
force. They are accelerated downward by gravity. They fall. Some examples are a home run ball, a golf drive,
objects falling from buildings, an artillery shell, and a dropped package.
We can make calculations about how they move.
Related quantities are;
- how far they go,
- how high they go,
- how long are they in the air,
- what is their velocity,
- what was their velocity when they started, and
- what was their velocity when they end
Recall the kinematic equations for bodies moving at constant acceleration with x = 0 at time = 0.
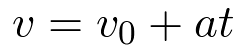
| (1) |
| (2) |
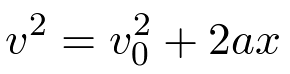
| (3) |
where a, v, x, and t are the acceleration, velocity, displacement in the x direction and
t = time.
These equations can be applied directly to
projectile motion. Neglecting air resistance, there is no horizontal force on a projectile. Projectiles move
at constant velocity in the x (horizontal) direction. Therefore,
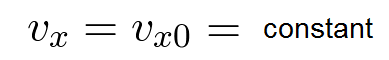
| (4) |
The horizontal velocity is equal to the initial velocity in the x direction. Also, since there is no acceleration
in the x direction,
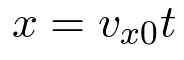
| (5) |
Motion in x and y are independent
The motion in the vertical (y) direction is independent of the motion in the horizontal (x) direction. There is an acceleration in the y direction. Objects fall toward the earth. On earth the acceleration in
the y direction is a constant,
equal to the negative gravitational acceleration.
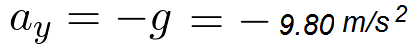
| (6) |
The kinematic equations for bodies moving in the vertical (y) direction under a constant gravitational acceleration
of -g are,
| (7) |
| (8) |
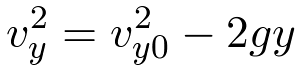
| (9) |
Example:
A football is kicked and leaves the ground at x = 0 at an angle of 30.0 degrees and a velocity of 25.0 m/s.
- How high does it go?
- How long is it in the air?
- Where does it Land?
The motion of the football in the y direction is independent of its motion in the x direction. We can solve for the
motion in the y direction using Equations 7, 8, and 9. What is the initial velocity in the y direction? To find this
we need to get y component of the initial velocity. vy0 = 25 sin(30o) = 12.5 m/s.
We can use equation 9 to find how high it goes. At the top of its trajectory, its velocity in the y direction is zero.
Solving equation 9 for the height, y, when the velocity in the y direction is zero,
The ball goes 7.97 meters into the air.
To find how long it is in the air, we can use equation 8. We want to know at what time the ball is on the ground.
To do this we set y equal to zero in equation 8.
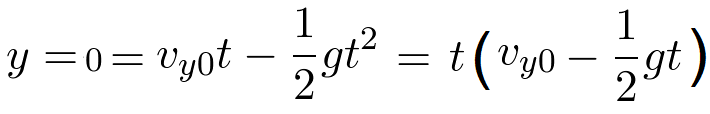
| (10) |
Equation 10 is equal to zero when the ball is on the ground. This occurs when time is zero just as the ball
is kicked and also, when the ball completes its trajectory and returns to the ground (y = 0).
Setting the term in the parenthesis equal to zero and solving for the time yields,
The ball is in the air for 2.55 s.
How far does the ball go? This is the distance in the x direction where it hits the ground.
This occurs at time t = 2.55 s.
The distance is the velocity in the x direction multiplied by the time. The component of the initial velocity
in the x direction is vx0 = 25 cos(30o) = 21.7 m/s.
The distance traveled is the velocity times the time x = 21.7 * 2.55 = 55.2m.
Problem
If the goal post is 45.0 meters away and 3 meters high,
how high is the ball if it clears the goal post?
