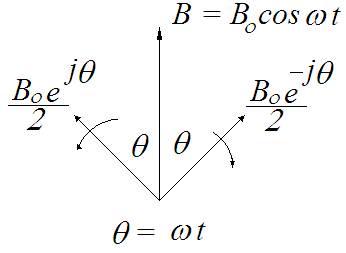


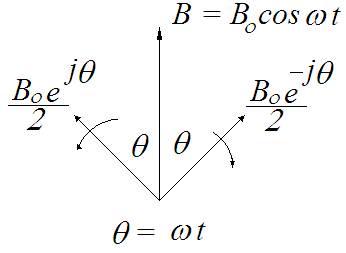



|
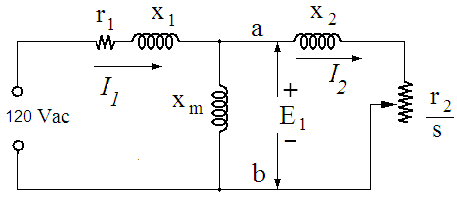
Efficiency and power factor are derived as a function of motor speed as expressed by the slip. This is done using the standard equivalent circuit, shown in Figure 4. Efficiency and power factor increase as slip decreases and the motor speed approaches the synchronous speed.
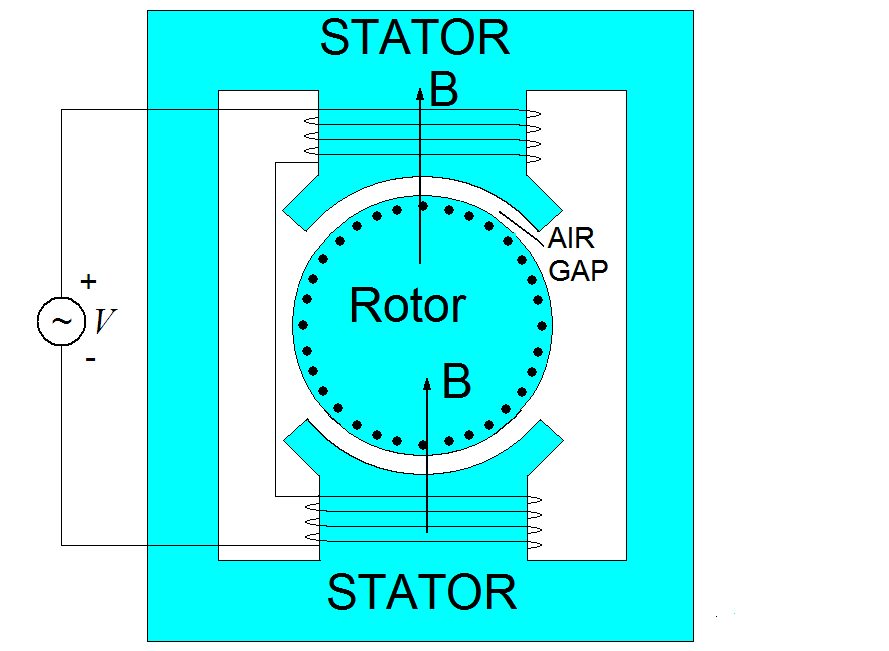
A representation of a single phase induction motor is shown in Figure 1. The line voltage V causes a current to flow in the stator winding. This current creates a magnetic field, B. The magnetic flux flows through the stator, rotor and the air gap.
Figure 2 shows a representation of the sinusoidally varying magnetic field, Bocos(wt). The magnetic field is in the vertical direction. It consists of two components, one rotating clockwise and the other rotating counterclockwise. Motor operation requires a rotating magnetic field. Rotor currents interacting with the rotating magnetic field generate the motor torque.
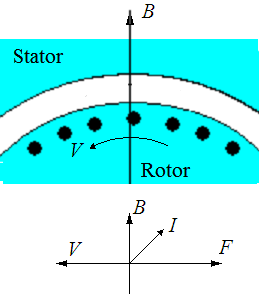
The physical mechanism that generates rotor torque is depicted in Figure 3. The clockwise rotating component of the magnetic field, B is shown. The rotor also rotates clockwise but at a slower rate. The relative motion of the rotor coil and the magnetic field causes a force on charges in the coil that results in coil current. The force on charges that causes coil current is,
where V , the velocity of the rotor coil relative to the magnetic field, is to the left. The force on charges in the rotor is perpendicular to both the B field and the velocity, V. This force results in the current, I, into the paper as shown in Figure 3.
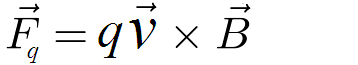
(1)
The rotor current flowing in the magnetic field experiences a second force given by,
where I , is the rotor current. and L is the length of the wire segment. This force is to the right in Figure 3. It is responsible for the rotor torque. This force causes the rotor to move in the direction of the passing rotating magnetic field. Both forces, F and Fq , are Lorentz forces that result from motion of charge relative to a magnetic field. F and Fq are perpendicular to each other.

(2)
Starting
When the magnetic field is not rotating, there is no torque generated. The magnetic field shown in Figure 3 is stationary. True, it has two rotating components, but their sum is stationary. An additional coil, the starting coil, is necessary. A starting stator winding is employed to produce a rotating magnetic field. The starter winding is perpendicular to the main stator winding. If the current in the starter winding were 90o out of phase with the main winding and if it produced a magnetic field of the same magnitude, the magnetic field in the, say x, direction would be B cos(w t) and the magnetic field in the y direction would be B sin(w t) . The result would be a rotating magnetic field. Typically the starter winding has a more resistive impedance than the main winding. The current in the starter winding is out of phase with the current in the main winding. This results in a rotating stator field that causes the motor to start. Once the rotor is rotating, it will interact with one of the rotating components of the magnetic field, shown in Figure 2, to produce torque. Typically the starter winding is switched out once the motor comes up to speed.
Slip
The rotating components of the magnetic field, shown in Figure 2, rotate at synchronous speed. Synchronous speed for the double pole motor shown in Figure 1 is 60 Hz or 3600 rpm. The rotor rotates at a speed less than the synchronous speed. The rotor sees a changing magnetic field that results in voltages and currents that produce torque. If the rotor is rotating at w radians per second in the forward direction and the synchronous speed is ws, then the rotor is traveling at a speed , ws - w
in the backward direction relative to the magnetic field. The slip is usually expressed as a fraction of the synchronous speed,
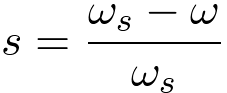
(3)
Motor Model
The interaction of the stator and the rotor windings is similar to that of the primary and secondary windings of a transformer. The rotor windings act like the secondary. The speed of the rotor relative to the rotating magnetic field is ws - w . If the rotor were rotating at synchronous speed, ws , it would see a constant magnetic field (zero frequency). There would be no voltage induced in the rotor and no rotor currents. The frequency of the magnetic field seen by the rotor is a fraction, s, of the frequency seen by the stator. The voltage induced in the rotor windings is proportional to the slip s.
The motor is like a transformer where impedances attached to the secondary can be referred to the primary. Rotor resistance r2 and reactance x2 are referred values from the rotor to the stator. Power delivered to the load is incorporated into the power dissipated in r2.
Since the induced voltage in the rotor is proportional to the frequency seen by the rotor and the voltage induced in the stator is proportional to ws, the rotor voltage referred to the stator is divided by the slip, s. E1 = E2 / s , where E1 is the back emf induced in the stator by the changing magnetic field and E2 is the equivalent emf induced in the rotor referred back to the stator. If the rotor were blocked, s would be one and the equivalent rotor voltage, referred to the stator, would equal the stator back emf, E1.
The impedance of the rotor is
where the reactance, x2, is multiplied by the slip fraction, s, to reflect the lower frequency seen by the rotor.
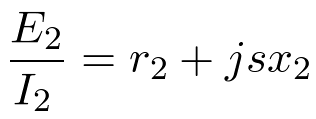
(4)
Since the rotor voltage is also less by a factor of s,
Solving for the rotor impedance referred back to the stator.
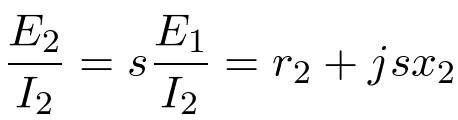
(5)
If the rotor is rotating at synchronous speed, s = 0. Then there is no slip and the rotor looks like an open circuit. If the rotor is blocked, s = 1. The equivalent rotor resistance is a minimum. Power delivered to the rotor is a maximum.

(6)
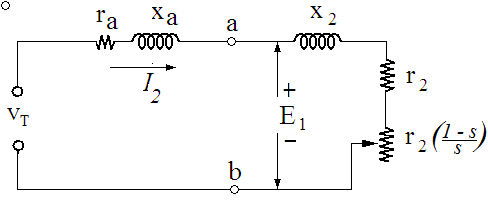
An equivalent circuit for the motor is shown in Figure 4. x1 is the stator leakage reactance. r1 is the stator resistance. xm is the magnetization reactance. It accounts for the current needed to set up the magnetic field. Once the magnetic field is set up, additional stator current is offset by rotor currents that act, by Lenz's law, to minimize changes in the magnetic field. The motor equivalent circuit is essentially the same as that of a transformer.
Efficiency
Power is torque multiplied by angular frequency. The magnetic field rotates at the synchronous angular velocity and exerts a torque. The power produced by this torque is proportional to the synchronous angular velocity.
where T is the torque and w s is the synchronous angular velocity.
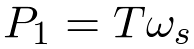
(7)
The rotor experiences this torque, but it rotates at the operating speed of, w. Therefore the mechanical power produced by the rotor is,
where w is the rotor angular velocity.

(8)
The inherent rotor efficiency is the mechanical power, P2 (Equation(8)) divided by the power delivered to the rotor, P1 (Equation(7)).
where equation 3 has been used. Equation 9 does not include ohmic and core losses.
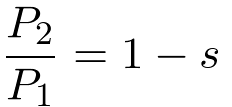
(9)
Ohmic and core losses can be included using the circuit in Figure 5. In Figure 5 there is just one loop. The same current flows in the elements representing the stator and in the elements representing the rotor. One loop has been achieved by Thevenizing the stator circuit looking toward the source from the terminal ab. Also, the rotor resistance r2 /s, is divided into two resistances. Mechanical power to the load is dissipated in the variable resistance. Power divides between the two resistors as predicted by Equation 9.
Since Xm is large, the Thevenin resistance ra is nearly equal to the stator resistance, r1. Since all the resistors in Figure 5 carry the same current, relative power is proportional to the values of resistances. The mechanical power delivered to the load is,
The power input to the motor from the power line is,
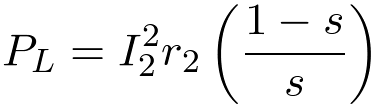
(10)
The efficiency is the power to the load, PL divided by the input power, Pin. The efficiency is,
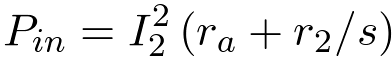
(11)
where ra is approximately equal to the stator resistance. r2 is the rotor resistance.
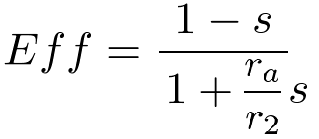
(12)
|
Figure 6 Efficiency as a function of slip is plotted using Equation 12. |
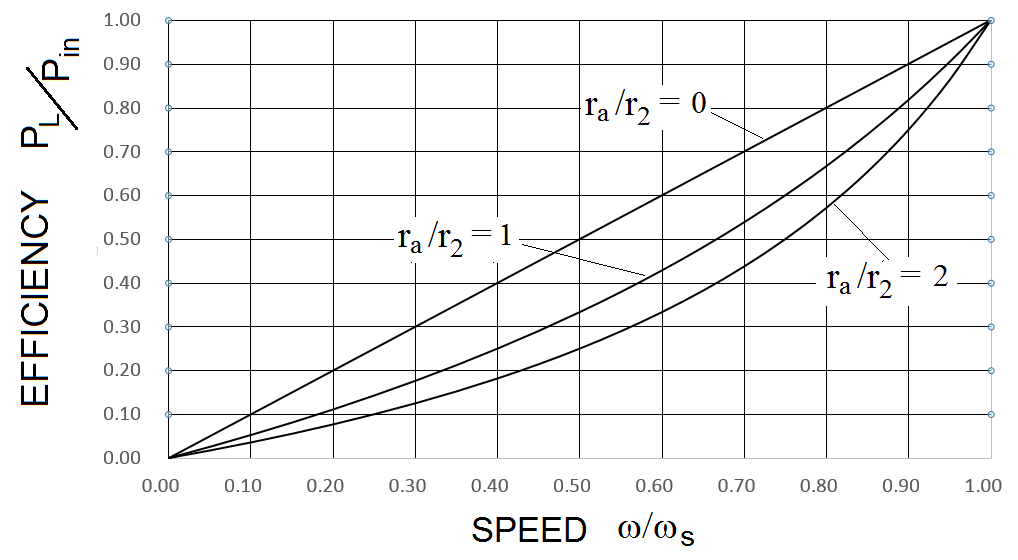
Figure 7 Since motor speed is a function of slip, w / ws = 1 - s , efficiency as a function of motor speed is shown by just flipping Figure 6's horizontal axis. |
Power Factor
The power factor is the ratio of the power absorbed from the power line to the volt-amperes absorbed. The power factor is the ratio of the resistance to the magnitude of the impedance that the motor presents to the power line. The power factor is,
From the circuit in Figure 6, R = ra + r2/s and X is the sum of the stator and rotor leakage reactances Xa + X2 . The power factor is,
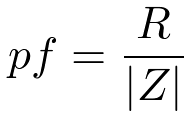
(13)
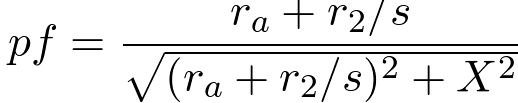
(14)
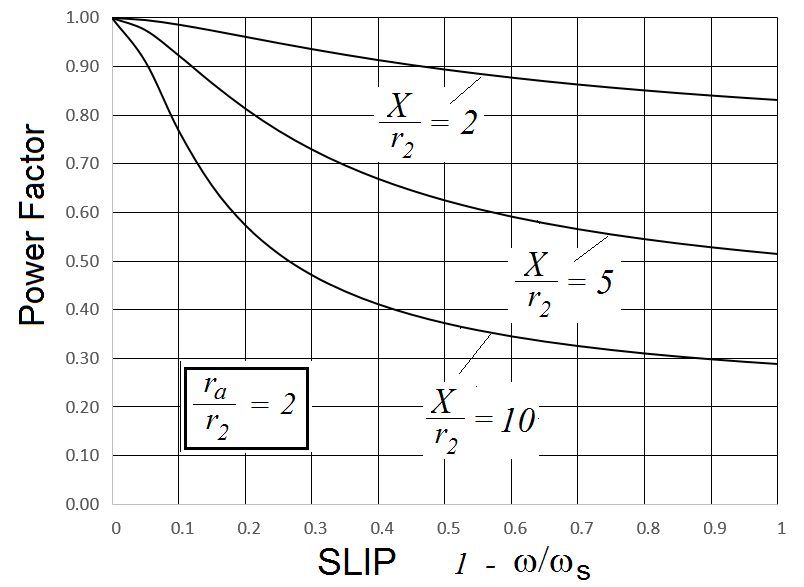
Figure 8 Power factor as a function of slip is plotted using Equation 14. |
Figure 9 Power factor as a function of motor speed is shown. |
Summary
Efficiency and power factor as a function of slip are given by Equations 12 and 14. The difference between the synchronous speed and the motor speed causes power loss. This results in an inherent efficiency of 1 - s . As slip increases efficiency decreases. Power factor also decreases as slip increases. The effect of motor parameters can be determined using Equations 12 and 13. Motor parameter values for the plots were chosen to represent typical cases.