Electrodes represent a coaxial cable
Electrodes represent a parallel plate capacitor
In this lab conductive sheets of paper are used to measure voltage as a function of position. That is, the voltage field produced by various configurations of charged electrodes is measured.
Electrodes are drawn on conductive paper using conductive ink. A power supply is used to establish voltages between electrodes. Current flows through the conductive paper, setting up a voltage field between the electrodes. A voltmeter measures values of the voltage field at positions between electrodes.
Knowledge of the voltage field allows the electric field and the current field to be calculated.
Equipment
| Electrodes represent a coaxial cable |
Electrodes represent a parallel plate capacitor |
Plotting equipotential lines
Current flows from the positive power supply terminal through the wire and contact to the drawn electrode. Current then flows through the resistive paper to the outer electrode, through the contact to the wire and back to the negative power supply terminal.
Due to resistance, there will be a voltage drop at the contacts and along the electrodes. We want to ignore these voltage drops. They should be small compared the voltage between the electrodes.
The theoretical expression for the voltage field between the inner conductor of radius, a, and the outer conductor, radius b, of a coaxial cable is;where r is the distance from the center and VBB is the power supply voltage.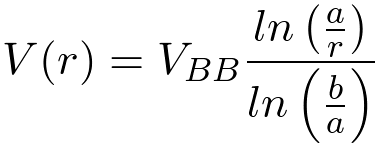
Electric field
The electric field is a vector. It is the negative gradient of the potential field. The x component of the electric field is,
Measure the potential at a point, then move, say one centimeter, and measure the potential again. The component of the electric field in the direction you moved is the change in voltage divided by the distance moved.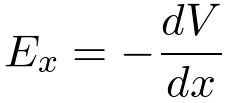
The units of the electric field are volts/meter.
The electric field is a vector, with three components. (We are concerned with only two components since we are working in only two dimensions.) The magnitude of the electric field is the maximum directional derivative of the voltage. The electric field is always in the direction of the maximum decrease voltage. Voltage determines electrostatic potential energy and charges experience forces that move them in the direction of lower potential energy.
Determine the magnitude and direction of the Electric Field 2.5 cm, 5.0 cm and 7.5 cm from the center.
Electric field lines
A complete field plot includes electric field lines. Electric field lines cross constant potential lines at 90o. The curvilinear rectangles formed by the electric field lines and the constant potential lines have approximately the same aspect ratio everywhere. The magnitude and direction of the electric field can be read from the electric field lines. The direction of the electric field at any point is tangent to the field line at that point. The density of the field lines gives the magnitude of the electric field. The field is stronger where the field lines are closer together.
Electric field lines are perpendicular to constant potential lines because the maximum change in potential is in the direction perpendicular to a constant potential line.
Once constant potential lines have been determined, electric field lines can be drawn.
The theoretical expression for the potential field is,
where VBB is the voltage of the upper plate relative to the lower plate, d is the distance between plates, and y is the distance of a field point from the lower plate.
Drawing electrodes
The line will dry in 3-5 minutes, but it will take 20 minutes to reach maximum conductivity.
Mount the conductive paper on the corkboard using stickpins at each corner.
Question to keep in mind