Sampling
The function x(t) is sampled at times t = kT. The sampled function y(t) can be represented
as the product of x(t) and a sampling function p(t).
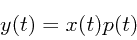 | 1 |
For impulse sampling,
 | 2 |
Combining equations 1 and 2.
 | 3 |
Since p(t) is a periodic function it can be represented by the Fourier series shown in equation 4.
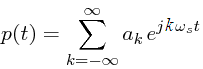 | 4 |
where for impulse sampling, ak = 1 / T.
 | 5 |
Multiplying equation 5 by x(t).
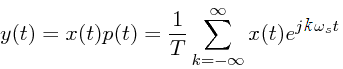 | 6 |
Multiplying a time function by 
results in a shift of kws
in the frequency domain. That is,
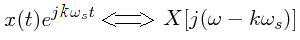 | 7 |
Applying equation 7 to equation 6 results in the following for the frequency spectrum of y(t) the sampled signal.
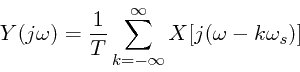 | 8 |
Consider a signal with the spectrum X(jw), of the baseband x(t).
The spectrum of the sampled function, Y(jw), contains duplicates of the baseband signal
shifted to multiples of kws , as shown below.
Aliasing
To avoid the overlap distortion called aliasing, wb must be less than
-wb + ws
That is,
ws > 2 wb
This result, that the sampling frequency must be at least twice the largest baseband frequency is called the
Sampling Theorem.
